We are trying to create machine learning models that not only perform well on training data but also generalize effectively to unseen examples. However, this pursuit often encounters a formidable adversary: overfitting, which occurs when a model learns to memorize the training data rather than capturing its underlying patterns and then apply it to new data. Of course this results in poor performance on new and unseen data. in order to fight this challenge, various regularization techniques have been developed, aiming to constrain the complexity of models and thereby enhance their generalization capabilities. One such technique that has gained widespread popularity and demonstrated remarkable effectiveness is dropout regularization.
Dropout regularization technique was introduced by Srivastava et al. ten years ago and offers a simple yet powerful approach to mitigating overfitting in neural networks. Unlike traditional regularization methods that penalize the magnitude of parameters, dropout operates by selectively disabling neurons during training, thereby encouraging the network to learn redundant representations of the data.
In this article, we will explore the underlying principles of dropout regularization, its mechanisms, and practical implications. We aim to provide a comprehensive understanding of how dropout works, why it is effective, and how it can be effectively implemented across various machine learning tasks and architectures.
Through a blend of theoretical insights, empirical evidence, and practical guidelines, we seek to equip readers with the knowledge and tools necessary to leverage dropout regularization as a potent weapon against overfitting, enabling the creation of more robust and generalizable machine learning models.
Let’s try to understand the dropout
Dropout regularization is a technique designed to mitigate overfitting in neural networks by randomly dropping out a fraction of neurons during training. This dropout process forces the network to become more robust by preventing reliance on specific neurons and learning redundant representations of the data. Let’s delve deeper into how dropout works and the intuition behind it.
How does the dropout works?
Dropout operates by randomly deactivating (or “dropping out”) a fraction of neurons in a neural network during each training iteration. This dropout is typically applied to hidden neurons, although it can also be applied to input neurons. During dropout, the dropped-out neurons are effectively removed from the network, meaning their outputs are set to zero. Consequently, the network is forced to adapt and learn from a different subset of neurons in each training iteration. By doing so, dropout prevents complex co-adaptations between neurons and encourages the network to learn more robust and generalizable features.
What is the intuition behind the dropout technique?
The intuition behind dropout stems from the concept of ensemble learning. Ensemble methods combine multiple models to produce better predictions than any individual model. Dropout can be seen as a form of ensemble learning within a single neural network. By randomly dropping out neurons, dropout effectively creates a multitude of “subnetworks” within the main network. During training, each subnetwork learns to make predictions independently, but they are all trained simultaneously.
This process encourages the network to generalize better, as it learns to rely on different combinations of neurons for making predictions.
At inference time (i.e., when making predictions), the predictions of all subnetworks are averaged or combined, leading to improved generalization performance.
Mathematical Formulation for Dropout Regularization Technique
Mathematically, we can represent the dropout during training like this:

And during interference like so:
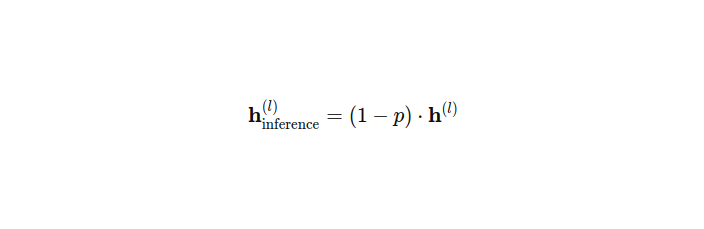
In essence, dropout applies a binary mask to the activations of each layer during training, effectively zeroing out a fraction of them. This stochastic process encourages the network to learn more robust features and prevents overfitting. During inference, these activations are scaled by 1- p and this ensures that the expected output remains the same as during training.
Let’s take a look at the training phase and dropping out neurons. During that phase, dropout regularization operates by randomly dropping out (i.e., deactivating) a fraction of neurons in each layer of the neural network. This dropout process is stochastic, meaning that different sets of neurons are dropped out in each training iteration. The dropout probability p determines the fraction of neurons to be dropped out. By doing so, dropout prevents the network from relying too heavily on specific neurons and encourages it to learn more robust features.
And then in the training phase, we also have forward and backward propagation with dropout. During forward propagation, when inputs are fed through the network, the dropout mask is applied to the activations of each layer. The dropout mask is a binary vector of the same size as the layer’s output, where each element is set to 0 (dropout) with probability p and 1 (retain) with probability 1−p. Element-wise multiplication between the dropout mask and the layer’s activations effectively drops out a fraction of the neurons.
During backward propagation, the gradients are backpropagated through the network as usual. However, since some neurons are randomly dropped out during forward propagation, only the active neurons (those retained by the dropout mask) contribute to the gradients. This means that the network learns to make predictions in a more robust and generalized manner, as it is forced to rely on different subsets of neurons in each training iteration.
And then during the inference phase (i.e., when making predictions on unseen data), dropout is not applied in the same way as during training. Instead, to maintain the expected output of the network, the activations of each layer are scaled by a factor of 1−p. This scaling ensures that the expected output remains the same as during training, effectively compensating for the dropout applied during training. By scaling the activations, the network’s predictions are consistent with what was learned during training, while still benefiting from the regularization effect of dropout.
What are the Benefits of Dropout Regularization
Dropout regularization offers several key benefits, including the prevention of overfitting, improvement in generalization performance, and enhanced robustness to noise in the data. By incorporating dropout into neural network training, practitioners can develop models that exhibit better performance and greater reliability across a wide range of machine learning tasks and domains. Let’s take a look at these benefits of dropout regularization a bit closer.
Prevention of Overfitting
Dropout regularization is highly effective in preventing overfitting, which occurs when a model learns to memorize the training data rather than capturing its underlying patterns. By randomly dropping out neurons during training, dropout prevents complex co-adaptations between neurons, forcing the network to learn more robust and generalizable features. This regularization technique encourages the network to become less sensitive to noise and outliers in the training data, ultimately leading to better performance on unseen data.
Improvement in Generalization Performance
One of the primary objectives of machine learning is to develop models that generalize well to unseen data. Dropout regularization significantly contributes to this goal by promoting the learning of diverse representations of the data. By randomly dropping out neurons, dropout effectively creates an ensemble of subnetworks within the main network, each of which learns to make predictions independently. During inference, the predictions of all subnetworks are combined or averaged, leading to improved generalization performance compared to a single deterministic model.
Robustness to Noise in the Data
Neural networks trained without regularization techniques are often sensitive to noise and outliers in the training data, leading to poor generalization performance. Dropout regularization enhances the robustness of neural networks by encouraging them to learn redundant representations of the data. By randomly dropping out neurons during training, dropout prevents the network from relying too heavily on specific features or patterns that may be noise-induced. As a result, the network becomes more resilient to noisy or corrupted data, leading to more reliable predictions on unseen examples.
What are Implementation Considerations when Working with a Dropout Technique?
Implementation considerations for dropout regularization include choosing the appropriate dropout rate, understanding its effects on training dynamics, and considering its impact on model architecture. By carefully tuning dropout parameters and integrating dropout into the model training process, practitioners can harness its regularization benefits to improve the performance and robustness of neural networks.
1. Choosing the Dropout Rate
Selecting an appropriate dropout rate is crucial for the effectiveness of dropout regularization. The dropout rate (p in the formula) determines the fraction of neurons to be dropped out during training. A common practice is to experiment with different dropout rates and evaluate their impact on model performance using validation data. Typically, dropout rates in the range of 0.2 to 0.5 are commonly used, but the optimal rate may vary depending on the dataset, model architecture, and specific task.
2. Effects of Dropout on Training Dynamics
Dropout regularization can influence the training dynamics of neural networks. Since dropout randomly deactivates neurons during training, it introduces noise into the learning process, which can lead to slower convergence and increased training time. Additionally, dropout may require higher learning rates or longer training epochs to achieve convergence compared to networks trained without dropout. Practitioners should monitor training progress, loss curves, and validation performance to assess the impact of dropout on training dynamics and adjust training parameters accordingly.
3. Impact on Model Architecture
Dropout regularization can have implications for the design and architecture of neural networks. When incorporating dropout into a model, it is essential to consider its placement within the network architecture. Dropout is typically applied to hidden layers, but it can also be applied to input or output layers, depending on the specific task and model design. Additionally, the choice of dropout rate may influence the overall architecture and complexity of the model. Designing effective architectures with dropout requires careful consideration of the trade-offs between regularization strength, model capacity, and computational efficiency.
What is the Empirical Evidence and Application of the Dropout Technique?
Dropout regularization has emerged as a versatile and effective technique for improving the generalization performance and robustness of neural networks across a wide range of machine learning domains and applications. Its empirical success and widespread adoption underscore its importance as a fundamental tool in the machine learning practitioner’s toolkit. Let’s take a look at the studies demonstrating the effectiveness of the dropout technique.
Studies Demonstrating the Effectiveness of Dropout
Numerous studies have demonstrated the effectiveness of dropout regularization across various machine learning tasks and architectures. For example, in their seminal paper, Srivastava et al. (2014) showed that dropout significantly improved the generalization performance of neural networks on tasks such as image classification and speech recognition. Subsequent research has further corroborated these findings, highlighting dropout as a powerful technique for preventing overfitting and improving model robustness.
Additionally, dropout has been shown to be effective in combination with other regularization techniques, such as L1 and L2 regularization, yielding even better performance gains. Research studies often benchmark dropout against other regularization methods and demonstrate its superiority in terms of generalization performance and robustness across diverse datasets and model architectures.
What are the Applications Across Various Domains
Dropout regularization has found wide-ranging applications across diverse domains, including but not limited to:
- Image Classification: Dropout has been extensively used in convolutional neural networks (CNNs) for tasks such as image classification, object detection, and segmentation. Dropout helps CNNs generalize better and achieve state-of-the-art performance on benchmark datasets like ImageNet.
- Natural Language Processing (NLP): In NLP tasks such as sentiment analysis, named entity recognition, and machine translation, dropout has been applied to recurrent neural networks (RNNs) and transformer-based models like BERT and GPT to prevent overfitting and improve model generalization.
- Reinforcement Learning: Dropout has been employed in reinforcement learning frameworks to enhance the learning stability and robustness of agents. By preventing overfitting and promoting exploration, dropout helps reinforcement learning agents generalize better across different environments and tasks.
- Time Series Analysis: In time series forecasting and anomaly detection, dropout has been used in recurrent neural networks (RNNs) and long short-term memory networks (LSTMs) to improve model generalization and robustness to noisy data.
Let’s Compare the Dropout Technique with Other Regularization Techniques
Contrast Dropout with L1 and L2 Regularization
L1 Regularization (Lasso) encourages sparsity by penalizing the absolute value of weights, promoting some weights to become zero. Dropout, in contrast, randomly deactivates neurons during training, fostering ensemble learning within a single network rather than enforcing sparsity.
L2 Regularization (Ridge) constrains weights by penalizing their squared magnitude, reducing model complexity. Dropout introduces noise by randomly dropping out neurons, encouraging robust and generalizable feature learning. While L2 regularization and dropout address different aspects of model complexity, they can complement each other.
What are the Differences from Other Dropout-like Techniques (e.g., DropConnect)
DropConnect extends dropout by randomly setting weights to zero instead of entire neurons. This approach regularizes by removing individual connections. Other techniques like DropBlock and SpatialDropout also modify network structure or connections randomly during training to prevent overfitting. However, dropout remains widely used due to its simplicity, efficiency, and proven effectiveness across various tasks and architectures.Practical Tips and Best Practices:
In conclusion
We’ve learned a lot and by following the practical tips listed in these article and the ones emphasized below you can effectively harness the power of dropout regularization to improve the generalization performance and robustness of your neural network models.
What are the Guidelines for Using Dropout Effectively?
- Start with Moderate Dropout Rates: Begin with moderate dropout rates (e.g., 0.2 to 0.5) and experiment with different values to find the optimal rate for your model and dataset.
- Apply Dropout to Hidden Layers: Dropout is typically applied to hidden layers rather than input or output layers. However, you can experiment with dropout at different layers to determine its impact on performance.
- Monitor Training Progress: Keep track of training progress, loss curves, and validation performance when using dropout. Adjust dropout rates and other hyperparameters based on performance metrics.
- Consider Dropout during Model Selection: When comparing models or selecting architectures, ensure that dropout is consistently applied and tuned across all models to make fair comparisons.
What are the Common Pitfalls to Avoid?
- Overusing Dropout: Applying dropout excessively or indiscriminately can lead to underfitting, where the model fails to capture important patterns in the data. Avoid using dropout rates that are too high, as they may hinder the learning process.
- Inconsistent Dropout Usage: Ensure that dropout is applied consistently during both training and inference phases. Failing to apply dropout during inference can lead to discrepancies between training and inference performance.
- Ignoring Computational Costs: While dropout is an effective regularization technique, it can increase computational overhead, especially for large models and datasets. Consider the computational costs of dropout when designing experiments or deploying models in production.
- Forgetting Other Regularization Techniques: Dropout is just one of many regularization techniques available. While dropout can be highly effective, it should be used in conjunction with other regularization methods (e.g., L1/L2 regularization) for optimal performance.